Macro view of NMR
Contents
- 1 Magnetism instead of transitions
- 2 Spectra vs Transition Spectra
- 3 Radio Pulse Power vs Transition Pulse Power
- 4 Saturation vs. Transition Saturation
- 5 Peak Intensity vs Transition Intensity
- 6 Sensitivity vs Transition Sensitivity
- 7 Peak Splitting vs Transition Peak Splitting
- 8 Relaxation vs Transition Relaxation
- 9 Related Topics
Magnetism instead of transitions
NMR at the level of the sample rather than the nucleus requires a complete change of thinking and a lot of math. The focus on the main page will be the thinking part, the math can be accessed on separate pages via links. The instrument utilizes magnetic induction rather than photon absorption. A transmitter causes changes in the magnetic fields of a sample, which then induce currents in a detector coil which are picked up by a receiver. So understanding NMR at a macro level requires intimate knowledge of magnetic moments and induction.
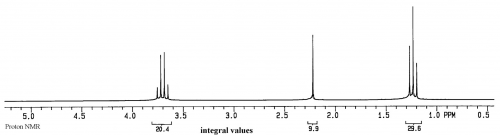
First the sample has to be defined. Ethanol is a good starting sample for analysis. It is a simple molecule, a liquid at room temperature with good flow rate (low viscosity) and slow evaporation rate (low vapor pressure). The molecule has 6 hydrogens, 2 carbons and an oxygen (CH3CH2OH), and there is not much self-association at room temperature. The sample container will be a 5mm glass tube:
About 0.75ml of ethanol in the tube will make a perfect sample for introduction to NMR.
All matter that is charged also has a magnetic field. Why? Good luck with that. Technically, if a charge isn't moving it isn't supposed to have a magnetic field, but since movement is relative, everything is moving compared to something else, so everything that is charged has a magnetic field. At any rate, since every atom has positively charged protons in the nucleus and negatively charged electrons surrounding the nucleus, there should be a net magnetic field around each atom. Similarly, there should be a net magnetic field around every molecule since the atoms are bonded to each other via electrons which all have charge and thus magnetic fields. However, a complication to this picture is that atoms and electrons also have a property called spin, and this property affects an atom's net magnetic field, and thus whether there is an actual net magnetic field.
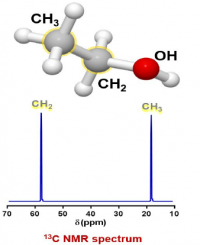
It turns out that the main 1H isotope of hydrogen (called proton in the NMR literature) and the 13C isotope of carbon (called carbon in the NMR literature) have net magnetic moments while the main isotope of oxygen and the main 12C isomer of carbon do not.
In summary, in the NMR tube of ethanol there is a solution of tiny bar magnets of 1H and 13C.
On the benchtop, the bar magnets floating around in solution are randomly oriented, so the bar magnets average out. If placed into a strong magnetic field however, some of the floating bar magnets will line up with the field, generating a net magnetic field for each 1H and 13C. If magnetism was the only factor then the floating bar magnets would line up with the external field and that would be it, nothing more would happen. The key part about NMR is that these magnets are also spinning, so there is torque that causes a precession around the axis of the external field. This precession frequency is what is probed with a transmitter.
Spectra vs Transition Spectra
To obtain a spectrum, the sample is placed into a static magnetic field to cause alignment of the magnets within a sample and their precession about the external magnetic field axis. This frequency depends on the gyromagnetic ratio (gamma) (g) for that element/elementary particle (a constant) and the intensity of the static magnetic field (B0) according to the derived equation:
v0=g*B0
Since this v0 is a moving charge, this represents electromagnetic frequency and can interact with an external electromagnetic frequency. In short, if an external electromagnetic frequency of the same magnitude is applied to the sample, it can 'resonate' with the sample, depending on the phases of the two fields. Fortunately, the gyromagnetic ratios of components of a sample are dramatically different, so a transmitter/receiver pair can be set up to 'look' at just one of the many v0 in a sample.
Based on the Larmor equation, the only variable for a particular atomic component is the external field strength B0, but since there are magnetic fields all around a molecule of the sample, each atomic component will experience slightly different B, and thus have slightly different v. Thus the transmitter/receiver pair will see several resonances for each atomic component in a sample of a molecule such as ethanol and it is these resonances that are studied in NMR. In addition, the atoms in a molecule that are in the same magnetic environment will experience the same B and thus have the same v and give the same peak.
For the sample of ethanol there are three groups of protons, and two groups of carbons, so there should be 3 peaks in the proton spectrum and 2 peaks in the carbon spectrum (the splitting in the proton spectrum and lack of splitting in the carbon spectrum will be discussed later):
For both spectra the x axis is relative frequency while the y axis is relative intensity.
Radio Pulse Power vs Transition Pulse Power
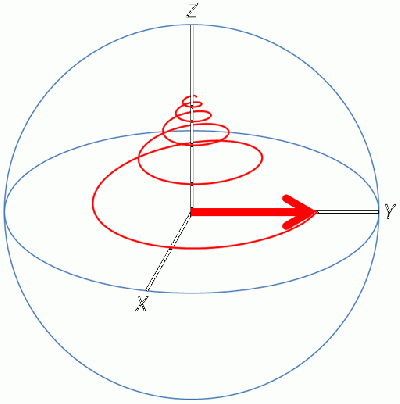
Radio pulse power is where the macro view of NMR changes dramatically from micro view. The situation at the start of an experiment is the sample suspended in a strong magnetic field, so any net magnetic dipoles start precessing around the external magnetic field axis, one for each group of net dipole atoms that are in the same environment. To make for easier presentation and graphing, only one dipole atom will be looked at, say one of the methyl protons of one molecule of ethanol in the sample that happens to line up with the external magnetic field.
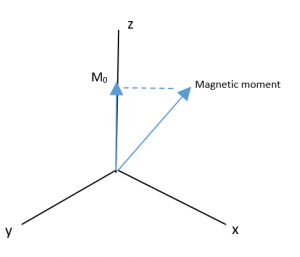
Since the magnetic moment is precessing, it is common to look at the Z-component of the equilibrium magnetic moment vector, called M0.
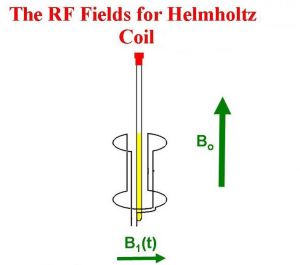
Then a transmitter in an axis orthogonal to the main magnetic field (B0) sends an Rf pulse, which creates a new magnetic field called B1:
The new magnetic field B1 pulls the M0 down into the XY plane. It rotates because the magnetic moment is rotating, and at the end of the pulse in the image, M0 is now along the Y axis.
Once the transmitter is turned off, the receiver is turned on and as M0 relaxes back to +Z again, the moving magnet induces a current in the receiver coil which is picked up as a signal in the detector. The signal is called a free induction decay because M0 is allowed to freely decay to its starting position, and while it returns it passes the receiver coil and induces a current.
Since the Rf is oscillating, the new magnetic field B1 cycles plus and minus and will cause M0 to push all the way to -Z and back up to +Z again, depending on how long the Rf pulse is. The detector only picks up magnetization on the XY plane, so as M0 vector goes to + or - Z, the signal goes to 0.
The receiver is along the X axis, so the pulse power to give the strongest signal is the one that pulls M0 down completely into the XY plane. This amount of pulse is called the 90 degree pulse, since it pulls M0 90 degrees from the Z axis. Pulse power is watts times time, and the watts is constant so the time is varied, with the resulting pulses given in microseconds. It is normal for the watts to be set such that the 90 degree pulse is between 5 and 10 microseconds, with the actual number determined experimentally for each dipole group.
For a 270 degree pulse, at the end of the pulse M0 is along the -X axis, which puts it 180 degrees out of phase compared to the 90 degree pulse.
For a 360 degree pulse, remember that the detector is not turned on until the end of the pulse, so even though M0 went all the way down to -Z and back up again, when the detector is turned on, M0 is back to +Z again so there is nothing to relax and thus no signal.
Saturation vs. Transition Saturation
Peak Intensity vs Transition Intensity
As seen in the section on radio pulse power, the intensity of the signal depends on the length of the Rf pulse used. Thus a group will give the highest intensity signal when measured in the XY plane if a 90 degree pulse is used for that group.
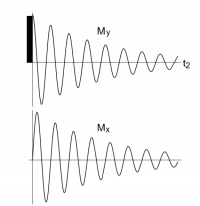
Once the transmitter is turned off and the receiver is turned on, the magnetization in the XY plane is given by the derived equations:
Mx = M0e-(t/T2)sin[(ω0-ω)t]
My = M0e-(t/T2)cos[(ω0-ω)t]
in these equations, as time t increases, the amplitudes of the sin/cos functions decrease because e-(t/T2) gets smaller as time gets larger. Note that M0, T2 and ω0 are constants. There is an Mx and My for each ω in the experiment
The signal picked up by the receiver is amplitude as a function of time over the experimentally set frequency range:
F(t) = My + iMx
This signal is then Fourier Transformed to give:
F(ω) = (M0T2)/2*[(1/(1+(ω0-ω)2T22)) + i((ω0-ω)/(1+(ω0-ω)2T22))]
In this equation there is no time component, so the result is a display of intensity (=F(ω)) vs frequency (ω). In addition, the only concentration term is M0, which represents the amount of magnetic moment for a particular group. As can be seen from the equation, the intensity of a peak is directly proportional to M0 and hence the concentration of the group represented by the peak. This means that the ratios of peak sizes for ethanol will be 3 for the methyl, 2 for the CH2 and 1 for the OH (30-20-10 in the spectrum of ethanol above).
Sensitivity vs Transition Sensitivity
Assuming that instrumental parameters are the same, a more concentrated sample will give a stronger peak.
Peak Splitting vs Transition Peak Splitting
The real weakness of net magnetization theory is its inability to explain peak splitting in coupled NMR spectra. The whole idea of 'net magnetization' is that it is a sum of the magnetic moments at each frequency, and there is just one sum! So how can there be peak splitting?